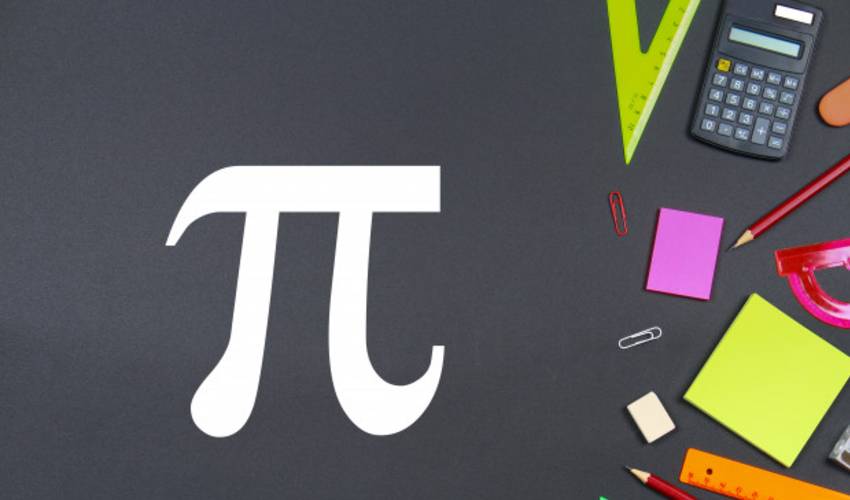El popular signo π se debe al matemático William Jones, quien usó la primera letra de la palabra griega “periferia” (πξριФξρια). Euler fue quien terminó de extender y generalizar este signo. El número pi (π) es la relación que existe entre las longitudes de una circunferencia y su diámetro. Se trata de un número irracional y es una de las constantes matemáticas más utilizadas. Es empleado en diversas áreas científicas tales como: la matemática, la física e ingeniería.
A lo largo de la historia, el valor de π se ha obtenido por medio de diversas aproximaciones. La relación entre la circunferencia y su diámetro no es constante en geometría no euclídeas. A continuación, te presentamos información relevante sobre este número y todas sus curiosidades.
Contenido
¿Qué es el número pi (π)?
Es la relación que existe entre la longitud de una circunferencia y su diámetro. Es un número irracional con números decimales infinitos y es una de las constantes de mayor importancia en las ciencias matemáticas.

La décima sexta letra del alfabeto griego es la letra pi. Además, es el símbolo asignado al número pi. Sus primeros diez decimales son: π = 3,1415926535…
Al ser un número irracional, esta constante tiene infinitos decimales y nunca se podrá calcularlos todos, es decir, es un proceso sin fin.
Historia
En Babilonia la relación entre la longitud de una circunferencia y su diámetro, fue asignada de una manera aproximada al valor 3. En el libro de las crónicas perteneciente a la Biblia, se representa como un recipiente circular que formaba parte del templo de Salomón. Su tamaño se especifica en la cita: “diez codos de ancho y un cordón de 30 codos lo ceñía a su alrededor”. Por lo tanto, al igual que la cultura de Babilonia era asignado el valor de 3 al número pi.
Posteriormente, los arquitectos fenicios y egipcios utilizaban el valor:
En la gran pirámide de Keops, la relación entre el perímetro de la base y su altura es aproximadamente el valor de 2π. Arquímedes de Siracusa colocó un cerco a la circunferencia, inscribiendo un polígono regular dentro del círculo y circundó otro del mismo número de lados por fuera. Cuanto mayor sea el número de lados de los polígonos más precisión tendremos.
Se empieza primero con un triángulo, después un cuadrado, pentágono, hexágono, etc. Al ir elevando el número de lados del polígono se aproxima a la circunferencia. Debido a esto, se puede aproximar lo que se desee con solo aumentar el número de lados.
Arquímedes obtuvo el siguiente valor, al usar un polígono de 96 lados:
El método de Arquímedes fue mejorado en China, en el siglo V. Cuando se descubrió la mejor aproximación en forma del número racional.
En el año 1596 el matemático holandés Ludolph van Ceulen dedicó toda su vida a calcular los decimales de pi, obteniendo 35 decimales.
Posteriormente, el año 1735 Euler resolvió el llamado “problema de Basilea”, obteniendo como resultado una suma infinita.
En el año 1699 Abraham Sharp calculó las 71 primeras cifras decimales de pi. Pero en 1761 el matemático alemán Lambert demostró que pi es irracional. Por su parte, el matemático inglés Shanks dedicó 20 años de su vida al cálculo de las 707 cifras decimales de pi. Sin embargo, cometió un error en el decimal 528 y posteriores. Circunstancia que solo se manifestó en el año 1949 con el empleo de cerebros electrónicos.
Shanks usó una serie ideada por Machin, que es la diferencia del desarrollo en serie de dos arcos tangentes.
Seguidamente, en el año 1882, Lindemann demostró que pi además de ser irracional es trascendente. Es decir, no puede ser solución de ninguna ecuación polinómica de cualquier grado de coeficientes reales. Por lo tanto, Lindemann puso punto final al problema de la cuadratura del círculo demostrando matemáticamente su imposibilidad.
Machin obtuvo 2.037 decimales de pi. Descubriendo el error cometido por Shanks, dos siglos y medio atrás. A partir de ese momento la búsqueda de los infinitos decimales de pi se convierte en un algoritmo de prueba de la velocidad de una computadora.
Aplicaciones
El número pi tiene una variedad de usos en nuestra vida cotidiana, entre ellos los más comunes son:
- En los relojes de péndulo que oscilan de un lado a otro.
- Teléfonos celulares, al transformar la voz en texto.
- En los cálculos que realizan los GPS para ubicar una posición en el mapa.
¿Qué podemos calcular?
Por medio del valor del número pi se pueden efectuar los siguientes cálculos:
- Circunferencias, conociendo el valor del radio o el diámetro con la fórmula: π2r = πd
- Áreas de círculos, conociendo el valor del radio con la fórmula: πr²
- Áreas de esferas, conociendo el valor del radio o el diámetro con la fórmula: 4πr² = πd²
- Volumen de esferas, conociendo el valor del radio con la fórmula: 4/3πr³
Algunas curiosidades del número pi
- Cada 14 de marzo se celebra el día internacional del número pi. Debido a que en la notación anglosajona se denota como 3/14.
- La longitud de los ríos, desde su nacimiento hasta su desembocadura. Además, de su longitud en línea recta es de aproximadamente 3,14.
- Este poema que ayuda a memorizar los veinte primeros dígitos del número pi, si cuentas la cantidad de letras de cada palabra:
“Soy y seré a todos definible
Mi nombre tengo que daros
Cociente diametral siempre inmedible
Soy de los redondos aros”.
- Las agujas de Buffon, hace referencia a un naturalista del siglo XVIII. Quien difundió el llamado método de la aguja para obtener el valor de π. Donde existía una superficie plana dividida en líneas paralelas separadas a una distancia constante H. Se toman algunas agujas y se dejan caer sobre la superficie. Se consideran caídas favorables cuando la aguja toca alguna de las rayas horizontales y caídas desfavorables cuando la aguja no toca ninguna de las rayas. Si se dividen los casos favorables entre el total de lanzamientos se obtenía el valor de π.
- En el año 1901 el matemático italiano Lazzerini, dejó caer la aguja 3408 veces obteniendo para pi el valor de 3,1415929 con un error de solo 0,0000003.